lab9¶
model(t, Ti, Ta, c)¶
We investigate a cup of tea.
Prerequisits: curve fitting, data analysis, inverting function (root find)
Preparation¶
In this lab, we will be using the curve_fit function from scipy,
which is located at scipy.optimize.curve_fit
Background¶
Enjoying a good cup of tea or coffee is an important part of our academic activities. Here, we study how a hot cup of tea or coffee cools down once the liquid has been poured into the cup.
A dedicated research unit in a little known university in central Java, Indonesia, has conducted temperature measurements for a cup of tea and made the data available:
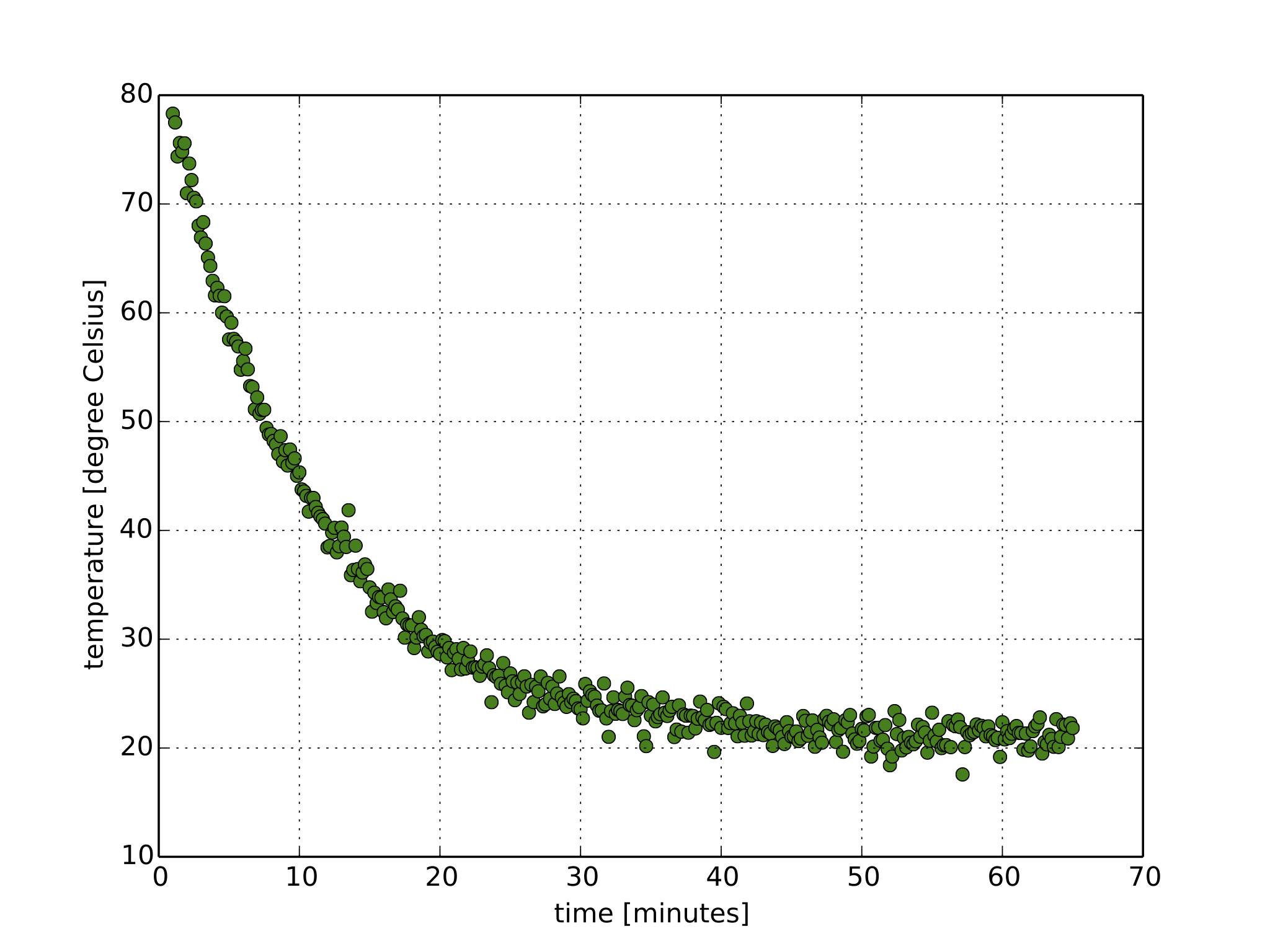
Temperature of cup of tea cooling down¶
The specialised equipment takes one temperature reading (in degree Celsius) every 10 seconds, although the measurements are somewhat noisy. Unfortunately, something went wrong in the beginning of the measurement, so the data for the first minute are missing.
Research questions¶
The questions we aim to answer are:
what was the initial temperature of the tea in the cup at time \(t=0\mathrm{s}\)?
how quickly does the tea cool down? In particular: after what time is it safe to drink it (we assume that 60C are a safe temperature).
what will be the final temperature of the tea if we wait infinitely long (presumably this will be the room temperature in this particular lab in Java).
Strategy¶
To make progress with this task, we define some variable names and have to make a few simplifying assumptions.
We assume that initial temperature, \(T_\mathrm{i}\), is the temperature with which the tea has been poured into the cup.
If we wait infinitely long, the final temperature will reach the value of the ambient temperature, \(T_\mathrm{a}\), which will be the environmental temperature in the lab where the measurements have been taken.
We further assume that the cup has no significant heat capacity to keep the problem simple.
We assume that the cooling process follows a particular model. In particular we assume that the rate with which the temperature \(T\) changes as a function of time \(t\) is proportional to the difference between the current temperature \(T(t)\) and the temperature of the environment \(T_\mathrm{a}\), i.e.:
We can solve this differential equation analytically and obtain a model equation:
where \(c\) is the time constant for the cooling process (which is expressed in seconds). The larger \(c\), the longer it takes for the hot drink to cool down. Over a period of \(c\) seconds, the drink’s temperature will decrease by approximately \(\frac{2}{3}\).
Exercise: model(t, Ti, Ta, c)¶
Implement a function model(t, Ti, Ta, c) which implements equation
(1).
We expect this behaviour:
In [ ]: model(0, 100, 0, 10) Out[ ]: 100.0 In [ ]: model(10, 100, 0, 10) Out[ ]: 36.787944117144235 In [ ]: import math In [ ]: math.exp(-1) * 100 Out[ ]: 36.787944117144235 In [ ]: model(10, 100, 100, 10) Out[ ]: 100.0 In [ ]: model(1000000, 100, 25, 10) Out[ ]: 25.0
\(\phantom{invisible white space}\)
The function
model(t, Ti, Ta, c)should return a single value iftis a floating point number, and an array iftis an array.Examples:
In [ ]: model(0, 100, 20, 500) Out[ ]: 100.0 In [ ]: from numpy import linspace In [ ]: ts = linspace(0, 3600, 4) In [ ]: ts Out[ ]: array([ 0., 1200., 2400., 3600.]) In [ ]: model(ts, 100, 20, 500) Out[ ]: array([ 100. , 27.25743626, 20.65837976, 20.05972686])
\(\phantom{invisible white space}\)
You can achieve this behaviour by using the exponential function from numpy (i.e.
numpy.exprather than the exponential function from themathmodule) when you implement equation (1) in the model function.
read2coldata(filename)¶
Reading data from columns in text file
Implement a function read2coldata(filename) which opens a text file
with name filename and which contains two columns of data. The
columns have to be separated by white space (such as one or more spaces
or tabs). The function should return a tuple of two numpy-arrays where
the first array contains all the data from the first column in the file,
and the second array contains all the data in the second column.
Example: for a data file testdata.txt which contains
1.5 4
8 5
16 6
17 6.2
we expect this behaviour:
In [ ]: read2coldata('testdata.txt')
Out[ ]: (array([ 1.5, 8. , 16. , 17. ]), array([ 4. , 5. , 6. , 6.2]))
In [ ]: a, b = read2coldata('testdata.txt')
In [ ]: a
Out[ ]: array([ 1.5, 8. , 16. , 17. ])
In [ ]: b
Out[ ]: array([ 4. , 5. , 6. , 6.2])
extract_parameters(ts, Ts)¶
Implement a function extract_parameters(ts, Ts) which expects a
numpy array ts with time values and a numpy array Ts of the same
length as the array ts with corresponding temperature values. The
function should estimate and return a tuple of the three model
parameters Ti, Ta and c (in this order) by fitting the model
function as in equation (1) to the data ts and Ts.
Hints:
The
curve_fitfunction may need some initial guesses (through the optional function parameterp0) for the model parameters to be able to find a good fit.You are strongly encouraged to plot your fitted curve together with the raw data to check that the fit is reasonable.
You can use a function like this:
import matplotlib.pyplot as plt
def plot(ts, Ts, Ti, Ta, c):
"""Input Parameters:
ts : data for time (ts) (numpy array)
Ts : data for temperature (Ts) (numpy arrays)
Ti : model parameter Ti for Initial Temperature (number)
Ta : model parameter Ta for Ambient Temperature (number)
c : model parameter c for the time constant (number)
This function will create a plot that shows the model fit together
with the data.
Function returns None.
"""
fig, ax = plt.subplots()
# plot the original data
ax.plot(ts, Ts, "o", label="data", alpha=0.3)
# compute a curve to plot based on the model
# and the parameters Ti, Ta and c for all points ts
fTs = model(ts, Ti, Ta, c) # fitted Ts
ax.plot(ts, fTs, label="fit")
ax.legend()
fig.savefig("compare-fit-and-data.pdf")
# plt.show() # to force pop-up window if desired
Research questions¶
Can you now answer (no need to submit these answers) the three research questions, i.e.
what was the initial temperature of the tea in the cup at time \(t\)=0s?
what will be the final temperature of the tea if we wait infinitely long (presumably this will be the room temperature in this particular lab in Java).
how quickly does the tea cool down? In particular: after what time is it safe to drink it (we assume that 60C are a safe temperature). (You can get this approximately from the plot, or exactly from the voluntary task
sixty_degre_time())
Additional (voluntary) tasks are available in lab9-extra.
End of lab9.